

A pyramid is a polyhedron with a polygon base and an apex with straight lines.The table below shows the properties of a pyramid: (BA = base area, P = perimeter, A = altitude, and SH = slant height ) Properties Regular hexagon base is called a hexagonal pyramid.Pentagon base is called a pentagonal pyramid.A quadrilateral base is called a square pyramid.Triangular base is called a Tetrahedron.Pyramids are typically described by the shape of their bases. It has a circular or oval base with an apex (vertex).Ī pyramid is a solid shape or a polyhedron with a polygon base and all lateral faces are triangles.The table below shows the properties of a cone where r denotes radius, h represents height and s represents slant height of the cone: Properties Based on how the apex is aligned to the center of the base, a right cone or an oblique cone is formed. It is formed by a set of line segments connected from the circular base to a common point, known as the apex or vertex. It has a flat surface and a curved surface, pointing towards the top. It is a three-dimensional object with two identical ends that are either circular or oval.Ī cone is a distinctive solid shape defined in a three-dimensional space.The bases are always congruent and parallel.The table below shows the properties of a cylinder: Properties It holds two parallel bases, circular in shape, joined by a curved surface(like a tube), at a fixed distance. All points on the surface are the same distance (r) from the center.Ī cylinder is a solid shape defined on a three-dimensional plane.

It is shaped like a ball and is perfectly symmetrical.The table below shows the properties of a sphere: Properties Every point on the surface is equidistant from the center. Let's explore types of solid shapes-Ī sphere is a solid shape, absolutely round in shape, defined in three-dimensional space.

These occupy some space, have length, width as well as height. Look around! Every other three-dimensional object, be it a laptop, cellphone, an ice-cream cone, balls, etc, are examples of solid shapes. Among them, analytic geometry and vector techniques have a major impact by allowing the systematic use of linear equations and matrix algebra, which are important for higher dimensions.Ī major application of solid geometry and stereometry is in 3D computer graphics.Solid shapes correspond to three-dimensional objects.
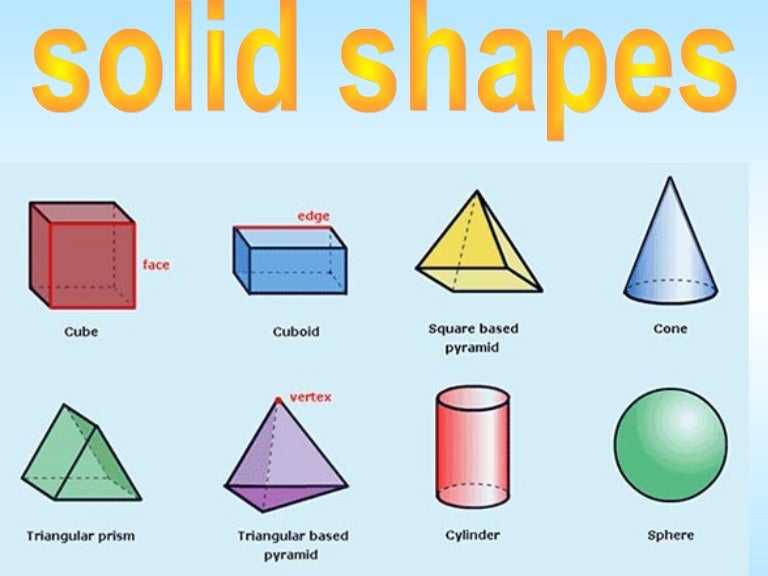
Various techniques and tools are used in solid geometry. Tri-axial ellipsoid (bottom right, a=4.5, b=6, c=3)Ī lens (or less than half of a circular arc) rotated about an axis passing through the endpoints of the lens (or arc) Ī surface that is generated by rotating a hyperbola around one of its principal axes įlat polygonal faces, straight edges and sharp corners or verticesĮxamples of ellipsoids with equation x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 : This more restrictive type of cuboid is also known as a rectangular cuboid, right cuboid, rectangular box, rectangular hexahedron, right rectangular prism, or rectangular parallelepiped. Some sources also require that each of the faces is a rectangle (so each pair of adjacent faces meets in a right angle).A convex polyhedron bounded by six quadrilateral faces, whose polyhedral graph is the same as that of a cube.A cube, except that its faces are not squares but rhombi.A parallelepiped where all edges are the same length.A prism of which the base is a parallelogram.A hexahedron with three pairs of parallel faces.A polyhedron with six faces ( hexahedron), each of which is a parallelogram.The following table includes major types of shapes that either constitute or define a volume. Whereas a sphere is the surface of a ball, it is sometimes ambiguous whether the term refers to the surface of the figure or the volume enclosed therein, notably for a cylinder. For a more complete list and organization, see List of mathematical shapes.


 0 kommentar(er)
0 kommentar(er)
